Το διάφραγμα και οι ρυθμίσεις του είναι κρίσιμης σημασίας στη φωτογραφία. Το διάφραγμα μαζί με τον χρόνο έκθεσης και τη ρύθμιση ISO, από τεχνική άποψη, αποτελούν τους τρεις “πυλώνες” για μία σωστή έκθεση του μέσου στο φως είτε πρόκειται για τον αισθητήρα των σύγχρονων ψηφιακών φωτογραφικών μηχανών είτε για το φιλμ. Ίσως η πιο σημαντική ρύθμιση είναι αυτή του διαφράγματος. Πάμε να δούμε γιατί.
Το διάφραγμα επηρεάζει πολλά διαφορετικά στοιχεία της φωτογραφίας όπως την ποσότητα του φωτός, το βάθος πεδίου αλλά και κάποια άλλα χαρακτηριστικά που σχετίζονται με τα οπτικά σφάλματα και τις εκτροπές του κάθε φακού άρα και την ευκρίνεια που θα πάρουμε στη φωτογραφία μας. Δεν είναι τυχαίο που πολλοί φωτογράφοι είτε χρησιμοποιούν χειροκίνητη λειτουργία στις μηχανές τους (Μ manual) είτε προτεραιότητα διαφράγματος (A aperture priority). Δεν θέλουν η μηχανή τους να επιλέγει αυτόματα το διάφραγμα.
Παρόλα αυτά, δεν θα ασχοληθούμε στο παρόν άρθρο με την έκθεση της φωτογραφίας, με τον “σωστό” φωτισμό της δηλαδή, ούτε με το βάθος πεδίου. Αυτά, από μόνα τους είναι ένα άλλο μεγάλο κεφάλαιο με πολύ ενδιαφέρον και πολλές εφαρμογές. Υπόσχομαι να το κάνω σε μελλοντικά άρθρα.

Τί είναι το διάφραγμα; Ποιες οι ρυθμίσεις του; Τι είναι ο αριθμός-f; Πώς προκύπτει; Τι είναι το f-στοπ και πώς σχετίζονται όλα αυτά με τη σωστή έκθεση της φωτογραφίας; Πότε λέμε έναν φακό “φωτεινό” ή “γρήγορο” και γιατί τα χαρακτηριστικά που έχει το διάφραγμα είναι σημαντικοί παράγοντες κόστους για έναν φακό;
Και υπάρχουν πολλά άλλα ερωτήματα που σχετίζονται με το διάφραγμα…
Είναι απαραίτητο να τα γνωρίζουμε όλα αυτά;

Θα προσπαθήσω να παρουσιάσω όσο πιο απλά γίνεται αυτές τις έννοιες αλλά και σε βάθος, όσο αυτός ο συνδυασμός απλότητας και λεπτομέρειας μπορεί να είναι εφικτός. Και πιστέψτε με, αυτή η προσπάθεια δεν είναι εύκολη. Και για εμένα που θα τα γράψω αλλά και για εσένα, τον αναγνώστη.
Θα μπορούσα να κάνω μία πιο απλή παρουσίαση, ίσως περισσότερο περιγραφική και λιγότερο αναλυτική (και με λιγότερα μαθηματικά) αλλά ο στόχος μου ήταν από την αρχή, να φτάσει αυτό το άρθρο σε ένα επίπεδο τέτοιο που θα μπορούσε να μείνει ως αρχείο στο ελληνικό διαδίκτυο για κάποιον που ενδιαφέρεται να μάθει κάθε πτυχή στο θέμα διάφραγμα, τόσο (και περισσότερο) για τον αρχάριο όσο και για τον προχωρημένο σε τεχνικά θέματα φωτογράφο.
Ξέρετε, πολλές φορές για να τεκμηριώσουμε κάτι, έχουμε το πρόβλημα της απλοποίησης. Και εκεί υπάρχει ο κίνδυνος, προσπαθώντας να κάνουμε τα πράγματα απλά και κατανοητά, να λέμε ανακρίβειες. Στο παρόν άρθρο, όσο μπορώ, προσπαθώ να απλοποιήσω τα πράγματα χωρίς να πέφτω στο σφάλμα να γράφω ανακρίβειες. Ή τελοσπάντων έτσι πιστεύω… Αν κάποιος πιο έμπειρος διαπιστώσει ανακρίβεια παρακαλώ να το επισημάνει στα σχόλια. Θα χαρώ πολύ. Τα γραπτά μένουν και επειδή πολλοί ενδεχομένως να τα διαβάσουν είναι κρίμα να υπάρχουν εσφαλμένες πληροφορίες.
Θα ήθελα λοιπόν την προσοχή σας! Και αυτό, γιατί για τον αρχάριο, οι πληροφορίες θα είναι πολλές και ίσως να μην χρειαστεί μόνο μία απλή ανάγνωση αλλά να διαβάσει το άρθρο με προσοχή, ως μελέτη. Από την άλλη θα ήθελα την προσοχή και των προχωρημένων σε τεχνικά θέματα φωτογράφων, για να εντοπίσουν τυχόν ανακρίβειες έτσι ώστε να μου τις επισημάνουν και να μείνει στο τέλος, κάτι χρήσιμο για όλους!
Η τεχνική επάρκεια του φωτογράφου
Πιστεύω πως ο φωτογράφος, για να φτάσει σε ένα επίπεδο και για να αρχίσει την απόπειρα να εκφραστεί μέσα από τη φωτογραφία, θα πρέπει τουλάχιστον, να έχει μία άρτια τεχνική επάρκεια. Αυτή η τεχνική επάρκεια θα τον βοηθήσει να επιταχύνει την πορεία του στον κόσμο της φωτογραφίας γιατί θα γνωρίζει πώς να χρησιμοποιήσει τον υπάρχοντα εξοπλισμό του, με τον καλύτερο δυνατό τρόπο για να αποδώσει με τον δικό του ξεχωριστό τρόπο “την εικόνα του κόσμου” που αυτός “είδε” και να ξεφύγει από μία απλή ή πιστή και μόνο, καταγραφή της πραγματικότητας.
Άλλωστε σήμερα με τις τόσες κινητές συσκευές και τις δυνατότητες απεικόνισης που έχουν αυτές, είναι πολύ εύκολο, ο καθένας από εμάς να κάνει μία πολύ επιτυχημένη και “ωραία” καταγραφή. Αυτόματα και χωρίς πολλές γνώσεις.
Αλλά πιστέψτε με, με τον καιρό, και εφόσον θα θελήσετε να ασχοληθείτε πιο σοβαρά με τη φωτογραφία, δεν μπορεί να μην γνωρίζετε τί είναι το διάφραγμα και πώς να το “χρησιμοποιήσετε” δημιουργικά. Δεν πρέπει να παραλείψουμε αυτό που όλοι θα έχετε ακούσει: Πως ο εξοπλισμός και δη, ο ακριβός εξοπλισμός ή ο πολύ καλός εξοπλισμός αν θέλετε, τόσο για το μέσο καταγραφής, την φωτογραφική μηχανή, όσο και για τους φακούς, δεν μας κάνει καλύτερους φωτογράφους.
Ίσως ναι, ο ακριβός εξοπλισμός, να μας κάνει τη ζωή λίγο πιο εύκολη. Αλλά πριν φτάσουμε σε ένα επίπεδο ώστε να γνωρίζουμε ακριβώς τον εξοπλισμό που χρειαζόμαστε για μία συγκεκριμένη εφαρμογή, θα πρέπει να έχουμε εξαντλήσει όλες τις δυνατότητες των συστημάτων που ήδη έχουμε. Διαφορετικά βαδίζουμε σε ένα μονοπάτι άγνοιας που θα μας φέρει πιο κοντά στην απογοήτευση και σε… άδειο πορτοφόλι, χωρίς ουσιαστικό λόγο. Το να γνωρίζουμε με κάθε λεπτομέρεια τους περιορισμούς που μας θέτει ο υπάρχον εξοπλισμός μας, είναι σημαντικό για να προχωρήσουμε. Και αποτελεί αυτό και μία πρόκληση. Δηλαδή το να γνωρίζουμε τους περιορισμούς αλλά παρ’ όλα αυτά, να συνεχίζουμε την προσπάθεια για να πετύχουμε το επιθυμητό αποτέλεσμα. Με ό,τι διαθέτουμε. Γι’ αυτό, η διάταξη του διαφράγματος, όπως και οι ρυθμίσεις του, είναι κάτι, που πρέπει να έχουμε καταλάβει πολύ καλά!

Ήρθατε λοιπόν εδώ, για να καταλάβετε το διάφραγμα και τι είναι αυτός ο αριθμός-f του διαφράγματος. Καλά να πάθετε. Αν νομίζετε πως θα σας το πω απλά, τότε, χάσατε. Δεν γίνεται να μιλήσουμε για τον αριθμό-f και να μην κάνουμε και λίγο φυσική και μαθηματικά. Αλλά πιστέψτε με, δεν είναι και ανώτερα μαθηματικά…
Τι είναι το διάφραγμα
Το διάφραγμα (diaphragm) είναι ένας μηχανισμός, μία λεπτή κατασκευή, αδιαφανής, με ένα άνοιγμα (aperture) στο κέντρο του. Ο ρόλος του διαφράγματος είναι να σταματήσει (stop) τη διέλευση του φωτός εκτός από αυτό που διέρχεται μέσα από το άνοιγμα, την οπή του. Με απλά λόγια δηλαδή, με το διάφραγμα, ελέγχουμε την ποσότητα του φωτός που περνάει μέσα από τον φακό μας.
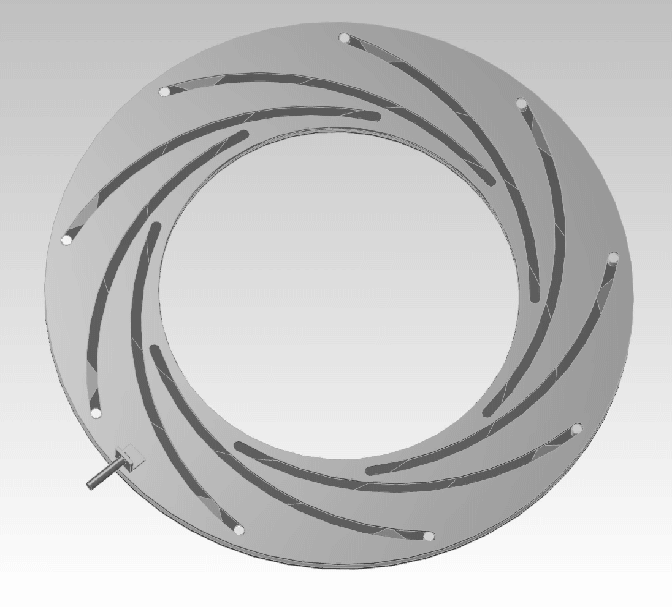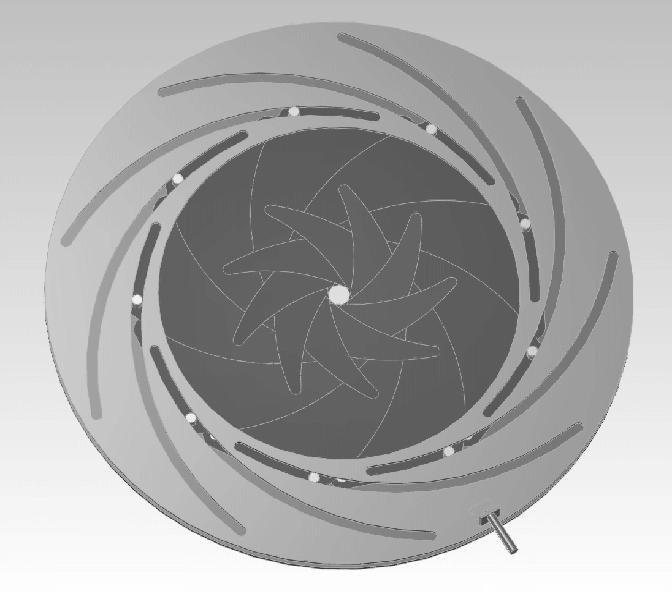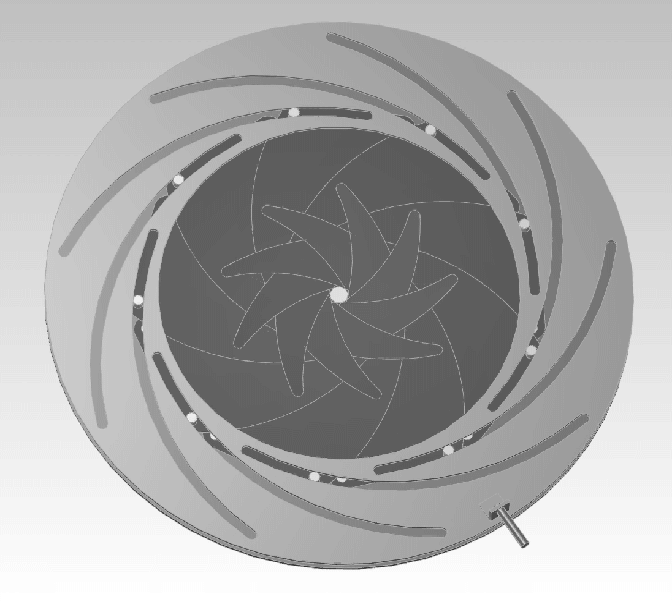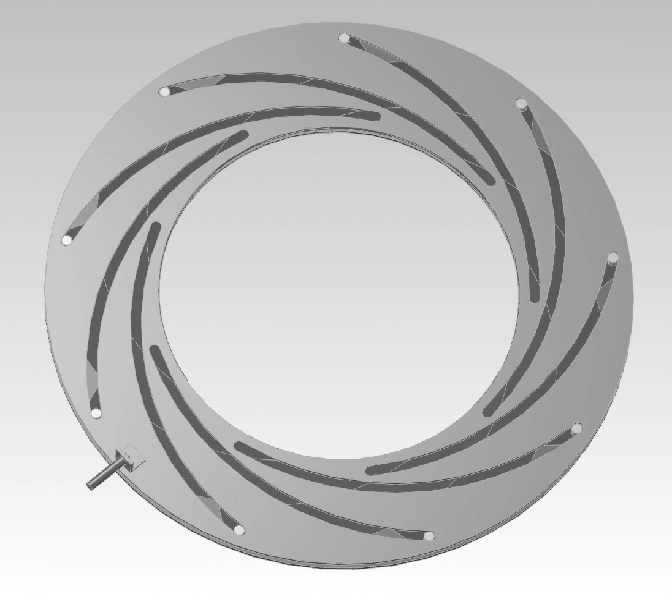
Όταν το διάφραγμα είναι ρυθμιζόμενο αυτό επιτυγχάνεται μέσω ενός μηχανισμού, της ίριδας, με “λεπίδες” που μπορούν να ανοίγουν και να κλείνουν σχηματίζοντας στο κέντρο τους μία τρύπα. Αυτή η οπή αποτελεί την κόρη της ίριδας του διαφράγματος. Ο μηχανισμός είναι κατασκευασμένος έτσι ώστε η κόρη, να έχει όσο το δυνατόν, κυκλικό σχήμα. Γι’ αυτό και χρησιμοποιούνται οι λεπίδες με το συγκεκριμένο σχήμα. Μάλιστα, το πόσες λεπίδες έχει η ίριδα του διαφράγματος ενός φακού, αποτελεί και ποιοτικό χαρακτηριστικό του.

Και ναι! Σωστά θα παρατηρήσατε. Ο μηχανισμός του διαφράγματος, ουσιαστικά μιμείται τη λειτουργία της ανθρώπινης όρασης. Όπως και τα μάτια μας με την ίριδα ρυθμίζουν τη φωτεινότητα, έτσι και το διάφραγμα. Και φυσικά σας προτρέπω να διαβάσετε για την ανθρώπινη όραση που μαζί με τον εγκέφαλο (δεν είναι μόνο τα μάτια) μας δίνουν μία “αναπαράσταση της πραγματικότητας” του κόσμου που μας περιβάλλει.

Και τα μάτια μας, ως οπτικό σύστημα είναι ένα τεράστιο κεφάλαιο. Να σας αναφέρω μόνο, πως επειδή το είδωλο απεικονίζεται σε σφαιρική επιφάνεια (και όχι σε επίπεδη όπως στις φωτογραφικές μας μηχανές) απαλλάσσει το μάτι από την ανάγκη για ιδιαίτερες κατασκευές στον φακό τους. Τεχνικές που βλέπουμε στους σύγχρονους φακούς, με σκοπό να διορθώσουμε τις εκτροπές τους και τις παραμορφώσεις τους.
Τον μηχανισμό του διαφράγματος, ρυθμιζόμενο ή μη θα τον συναντήσουμε σε πολλά ακόμα οπτικά συστήματα, όχι μόνο στη φωτογραφία. Για παράδειγμα στα τηλεσκόπια και στα μικροσκόπια. Θα ασχοληθούμε όμως εδώ μόνο με το διάφραγμα για τους κοινούς φωτογραφικούς φακούς.
Τί είναι ο αριθμός-f
Ένας “λόγος” είναι ο αριθμός-f. Να το πούμε κλάσμα; Χμ, ΟΚ, όπως θέλετε αλλά το σωστό είναι λόγος. Πάμε να τον ορίσουμε πρώτα και μετά, σιγά σιγά, θα αποκαλύψουμε τα “μυστικά του” και πόσο σημαντικός είναι για τη φωτογραφία, αλλά και γιατί (επιτέλους) πρέπει να τον γνωρίζουμε. Να τον γνωρίζουμε καλά, πολύ καλά!
Πριν ξεκινήσω να πω κάτι. Καλό είναι να είμαστε σωστοί στις εκφράσεις που αφορούν την ορολογία της φωτογραφίας. Και επειδή έχω ακούσει πολλές φορές να λέμε εμείς οι φωτογράφοι (τρομάρα μας) «το f» και «αυξάνω το f» και «βάζουμε μεγάλο f», να σας θυμίσω πως είναι λάθος να αναφερόμαστε στον αριθμό-f με ένα σκέτο f (εφ) ή λέγοντας πάλι έναν αριθμό σκέτο π.χ. “έβαλα διάφραγμα 16”. Έχει σημασία το πώς αναφερόμαστε στον αριθμό-f, το πώς ακριβώς “τον δηλώνουμε”.
Και επειδή είναι, «ο» αριθμός, αρσενικό δηλαδή, αρσενικός είναι και ο αριθμός-f. Δεν είναι τυχαίο που οπουδήποτε αναφέρομαι στον αριθμό-f, βάζω πάντα μπροστά τη λέξη «αριθμός». Γιατί έτσι πρέπει να αναφερόμαστε σε αυτόν και καλό είναι να μην τον αφήνουμε “ορφανό”. Επίσης, κατά αυτόν τον τρόπο, δεν μπερδευόμαστε όταν αναφερόμαστε στη σχέση που έχει ο αριθμός-f με το διάφραγμα, που είναι ουδέτερο.
Και ναι, πράγματι, ο αριθμός-f, σχετίζεται με το διάφραγμα αλλά δεν είναι το διάφραγμα. Είναι χαρακτηριστικό του.
Και συγκεκριμένα: χαρακτηριστικό που σχετίζεται με τη διάμετρο του ανοίγματος, της οπής του. Και επαναλαμβάνω εδώ πως έχει πολύ μεγάλη σημασία το πώς τον εκφράζουμε: σκέτο τον αριθμό-f ή στη μορφή ως κλάσμα f/N όπως θα δούμε και παρακάτω. Είναι αυτό, ένα από τα “μυστικά” του αριθμού-f που σας έλεγα πριν. Και πάλι υπομονή, θα το ξεδιαλύνουμε αυτό στη συνέχεια, μετά τον μαθηματικό του ορισμό, που ίσως αυτό είναι που προκαλεί τη σύγχυση και πολλοί είναι αυτοί που μπερδεύονται.
Αρκεί να θυμόμαστε όπως είπαμε, πως το σωστό, όταν αναφερόμαστε στον αριθμό-f, είναι να μην τον κάνουμε… ουδέτερο. Π.χ. πρέπει να λέμε «θα αυξήσω τον αριθμό-f», ή ρωτάμε: «ποιον αριθμό-f έχεις βάλει στη μηχανή σου;», ή «βάλε μικρότερο αριθμό-f για να έχεις bokeh» κ.ο.κ. όχι σκέτο f, ούτε σκέτο αριθμό.
Τι; ήρθατε εδώ για να μάθετε για το διάφραγμα; Υπομονή, έχουμε δρόμο ακόμα. Δεν γίνεται χωρίς θεωρία… και πάμε ευθύς αμέσως να ορίσουμε αυτόν τον αριθμό.
Ο μαθηματικός ορισμός του αριθμού-f
Ο αριθμός-f λοιπόν, ας τον πούμε Ν (από το Number) ορίζεται από τη σχέση:
Αριθμός-f = \LARGE N=\frac{f}{D}
Και αμέσως έρχεται το μπέρδεμα:
Μην μπερδευτείτε από εκείνο το \large f στον αριθμητή του κλάσματος. Δεν είναι αυτός ο αριθμός-f αλλά η εστιακή απόσταση. Ο αριθμός-f είναι το «Ν». Πάμε να δούμε τι είναι το καθένα από αυτά (και επιτρέψτε μου να αναφέρω και την αγγλική ορολογία):
\large N είναι ο αριθμός-f (f-number, f-stop, focal ratio ή f-ratio)
\large f είναι η εστιακή απόσταση του φακού (focal length), και
\large D είναι η διάμετρος της κόρης εισόδου (entrance pupil diameter)
Και με λόγια:
Στον κλάδο της φυσικής (που ονομάζουμε οπτική) ο αριθμός-f σε ένα οπτικό σύστημα (όπως π.χ. ένας φακός φωτογραφικής μηχανής) είναι ο λόγος της εστιακής απόστασης του συστήματος προς τη διάμετρο της κόρης εισόδου.
Ο αριθμός-f αναφέρεται και ως “εστιακός λόγος”, “λόγος-f” ή και “f-στοπ”. O αριθμός-f είναι αδιάσταστος, δεν έχει μονάδες μέτρησης (δεν είναι δηλαδή χιλιοστά, μέτρα, ή κιλά, σε αντίθεση με τον χρόνο για παράδειγμα, που έχει μονάδα μέτρησης το δευτερόλεπτο).
Και επίσης, ας προσέξουμε εδώ τις λέξεις:
Στον ορισμό του αριθμού-f, δεν είπαμε η «εστιακή απόσταση του φακού» αλλά η «εστιακή απόσταση του συστήματος». Και αυτό, γιατί συνήθως, ένας φωτογραφικός φακός αποτελείται από πολλά στοιχεία (από πολλά γυαλιά, φακούς δηλαδή) για να εξυπηρετήσουν συγκεκριμένες απαιτήσεις. Γι’ αυτό λοιπόν όταν αναφερόμαστε στην “εστιακή απόσταση ενός φακού”, εννοούμε φυσικά, την εστιακή απόσταση όλου του συστήματος φακών που βρίσκονται μέσα στον φωτογραφικό φακό μας.

Τώρα, δώστε λίγη παραπάνω προσοχή στο παρακάτω:
Ο αριθμός-f δηλώνεται συνήθως με τη χρήση του πεζού γράμματος f με τη μορφή f/N, όπου N είναι ο αριθμός-f. Για παράδειγμα αν έχουμε αριθμό-f = 2.8 γράφουμε f/2.8. Γιατί αλήθεια να το κάνουμε αυτό;
Να λοιπόν που εδώ “κρύβεται” ένα από τα μεγαλύτερα “μυστικά” του αριθμού-f. Δηλαδή ο τρόπος που τον εκφράζουμε ή που τον συμβολίζουμε αν θέλετε, και το τι ακριβώς δηλώνουμε όταν εκφράζουμε τον αριθμό-f σε μορφή κλάσματος f/N. Εκεί είναι το όλο θέμα.
Υπομονή όμως σε αυτό, πριν προχωρήσουμε, θα αναφέρουμε πρώτα, τί είναι εκείνη η διάμετρος D της “κόρης εισόδου”. Ωστόσο, εκείνο που πρέπει να παρατηρήσετε από τον μαθηματικό ορισμό, είναι ότι ο αριθμός-f είναι αντιστρόφως ανάλογος της διαμέτρου του διαφράγματος. Και αυτή η αντιστροφή, δηλαδή όταν το ένα μέγεθος μεγαλώνει, το άλλο μέγεθος μικραίνει, μας μπερδεύει. Κρατήστε όμως στο μυαλό σας τα δύο μεγέθη με τα οποία “παίζεται” εδώ το παιχνίδι. Το ένα είναι ο αριθμός-f, και το άλλο μέγεθος, είναι η διάμετρος (του ανοίγματος). Το τρίτο μέγεθος, η εστιακή απόσταση, δεν μας απασχολεί γιατί είναι ένα μέγεθος σταθερό (τουλάχιστον για τους σταθερούς φακούς. Θα δούμε τί συμβαίνει για τους φακούς zoom, που μεταβάλλεται η εστιακή τους απόσταση, αλλά μην τα βάλουμε όλα μαζί και “χάσουμε τη μπάλα”…)
Η κόρη εισόδου του φακού D
Η κόρη εισόδου ενός φακού, είναι η διάμετρος της οπής του διαφράγματος, όχι απαραίτητα όμως η φυσική διάμετρος, αλλά η διάμετρος όπως αυτή φαίνεται από την πλευρά “εισόδου” του φακού. Γι’ αυτό και την λέμε κόρη εισόδου (γιατί υπάρχει και η κόρη εξόδου).

Θα επιμείνω λίγο σε αυτό για να γίνει κατανοητό. Συνήθως, μπροστά από το διάφραγμα ενός φακού, υπάρχει ένα στοιχείο (ένα γυαλί, ένας φακός) που μπορεί την οπή του διαφράγματος να την κάνει να “φαίνεται” μεγαλύτερη όταν την κοιτάζουμε με τα μάτια μας από μπροστά. Για αυτήν ακριβώς την διάμετρο μιλάμε και όχι για την πραγματική διάμετρο της οπής. Όπως δηλαδή “φαίνεται” από την μπροστινή πλευρά του φακού και όχι η φυσική διάμετρος της οπής του διαφράγματος που θα μπορούσαμε να μετρήσουμε, αν αποσυναρμολογήσουμε τον φακό.
Η παρακάτω εικόνα εξηγεί λεπτομερέστερα τους όρους “κόρη εισόδου” και “κόρη εξόδου”. Στη λεζάντα θα βρείτε και τον ορισμό της κόρης εισόδου αλλά εσείς αρκεί να θυμάστε πως η διάμετρος της κόρης εισόδου, κατά κανόνα, είναι διαφορετική από τη φυσική διάμετρο. Την “Kόρη εισόδου” στα αγγλικά, θα την συναντήσετε ως “Entrance pupil“.
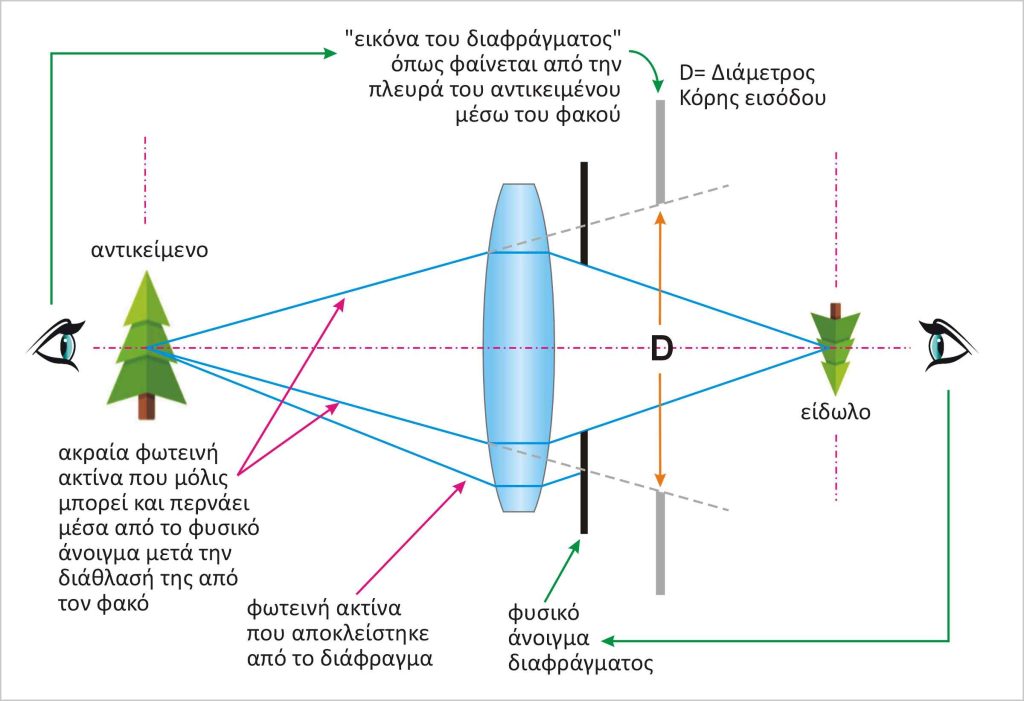
Η παραπάνω εικόνα είναι ένα απλοποιημένο παράδειγμα για να είναι εύκολα κατανοητό. Στην πράξη ένας φωτογραφικός φακός συμπεριλαμβάνει πολύ περισσότερα στοιχεία (“στοιχεία” εννοούμε γυάλινα στοιχεία, δηλαδή φακούς) .
Παρατηρούμε ότι αυτό το οπτικό σύστημα αποτελείται μόνο από έναν συγκλίνοντα φακό (σιέλ στο σχήμα) και το διάφραγμα.
Αν κοιτάξουμε τον φακό από μπροστά, βλέπουμε ότι το “φυσικό άνοιγμα” του διαφράγματος βρίσκεται πίσω από το φακό (με μαύρο χρώμα).
Μπορούμε επίσης να παρατηρήσουμε πως το φως που περνάει μέσα από αυτό το φυσικό άνοιγμα είναι περισσότερο από το φως που θα περνούσε αν ο φακός δεν υπήρχε στο σύστημα. Και αυτό, γιατί χωρίς τον φακό, δεν θα είχαμε φωτεινές ακτίνες που διαθλώνται, που συγκλίνουν.
Τώρα, αν παρακολουθήσουμε μία φωτεινή ακτίνα που διαθλάται από τον φακό, και που μόλις μπορεί και περνάει μέσα από το άνοιγμα και την ονομάσουμε “ακραία” φωτεινή ακτίνα και εντοπίσουμε την προβλεπόμενη διαδρομή της χωρίς τον φακό, τότε μπορούμε να ορίσουμε ως “κόρη εισόδου” το απαιτούμενο μέγεθος του ανοίγματος έτσι ώστε να μπορέσει να περάσει αυτή η “ακραία” ακτίνα φωτός. Έτσι στην παραπάνω εικόνα, η κόρη εισόδου, είναι μεγαλύτερη από το φυσικό άνοιγμα (η κόρη εισόδου φαίνεται με γκρίζο χρώμα).
Όσο αφορά τώρα την “κόρη εξόδου”, σε αυτό το παράδειγμα, είναι ακριβώς ίδια με το φυσικό άνοιγμα, δηλαδή η διάμετρος της κόρης εξόδου είναι ίση με τη διάμετρο του ανοίγματος του διαφράγματος επειδή δεν παρεμβάλλεται φακός μεταξύ της εικόνας και του ανοίγματος. Με άλλα λόγια κοιτάζοντας τον φακό από πίσω, βλέπουμε το άνοιγμα του διαφράγματος όπως είναι στη φυσική του μορφή.
Το “έχουμε” μέχρι εδώ;
Ωραία! Πάμε να δούμε ένα παράδειγμα:
Η αντιστροφή του αριθμού-f σε σχέση με τη διάμετρο της κόρης εισόδου
Ας υποθέσουμε ότι έχουμε έναν φακό με εστιακή απόσταση ίση με 10 χιλιοστά (f=10mm) και η διάμετρος της κόρης εισόδου του διαφράγματος είναι 5 χιλιοστά (D=5mm).
Τότε ο αριθμός-f θα είναι N=\large\frac{f}{D}=\large \frac{10mm}{5mm}=2. Και για να το γράψουμε πιο σωστά ή μάλλον για να δηλώσουμε σωστά τον αριθμό-f θα τον εκφράσουμε ως κλάσμα f/2.
Προσέξτε τώρα και το παρακάτω, που προκύπτει από τον ορισμό του αριθμού-f:
Αν γνωρίζαμε τον αριθμό-f (που είναι ίσος με 2) και δεν γνωρίζαμε την διάμετρο της οπής του διαφράγματος τότε μπορούμε να λύσουμε την παραπάνω σχέση του ορισμού του αριθμού-f, ως προς τη διάμετρο:
H διάμετρος της οπής του διαφράγματος D σε χιλιοστά, θα είναι: D=\frac{f}{N}mm. Ή αλλιώς: D=\frac{f}{αριθμός-f}mm. (Ξεχωρίστε και πάλι εδώ το f που είναι η εστιακή απόσταση, από τον αριθμό-f που είναι το Ν).
Φαίνεται λοιπόν ξεκάθαρα η αντιστροφή των δύο μεγεθών από τις παρακάτω σχέσεις:
αριθμός-f=\frac{f}{Διάμετρος} ⇒ Διάμετρος=\frac{f}{αριθμός-f}mm
Ας πάρουμε μία ανάσα από τα πολλά μαθηματικά. Το ξέρω πως πολλοί από εσάς όταν βλέπετε μαθηματικούς τύπους κάπως σας φαίνεται. Αν δεν το έχετε “πιάσει” μέχρι εδώ θα σας γίνει πιο καθαρό πιο κάτω.
Λοιπόν, πριν δούμε γιατί αυτός ο αριθμός μας φαίνεται «περίεργος» αξίζει να επιμείνουμε με αυτή την “αντίστροφη” επίδραση που έχει και πολλοί μπερδευόμαστε. Θα τον εξετάσουμε από κάθε άποψη….
Η “ανατομία” του αριθμού-f
Η πλειοψηφία των φακών που έχουμε για τις φωτογραφικές μηχανές διαθέτουν διάφραγμα ρυθμιζόμενο, δηλαδή έχουμε τη δυνατότητα να ανοίγουμε και να κλείνουμε την οπή της κόρης εισόδου ανάλογα με τις ανάγκες μας. Και οι ανάγκες μας είναι, κυρίως, η ρύθμιση της ποσότητας του φωτός που θα περάσει μέσα από τον φακό μας. Η ποσότητα του φωτός είναι αναγκαίο να είναι αυτή που πρέπει, (ή αυτή που θέλουμε) για να πετύχουμε σωστή έκθεση (ή την έκθεση που έχουμε σχεδιάσει). Και όταν ανοίγουμε ή κλείνουμε την οπή τί αλλάζει; Εφόσον δεν αλλάζουμε την εστιακή απόσταση π.χ. δεν κάνουμε ζουμ με τον φακό μας, εκείνο που αλλάζει είναι ο αριθμός-f.
Είδαμε πως: Κλείνουμε την τρύπα, μεγαλώνει ο αριθμός-f. Ανοίγουμε την τρύπα μικραίνει ο αριθμός-f.
Και αυτό μας μπερδεύει. Τι τον θέλαμε ετούτο τον αριθμό-f που όλο σε μπελάδες μας βάζει;
Μα δεν θα μπορούσε ίσως να γίνει καλύτερα. Είναι “ωραίος” ο αριθμός-f. Πριν όμως δούμε πώς τον χρησιμοποιούμε να πούμε δύο πραγματάκια ακόμα, το ένα έρχεται από τα μαθηματικά, το άλλο έχει σχέση με την ορολογία και πώς μπορεί αυτή να μας μπερδέψει όταν δεν την χρησιμοποιούμε σωστά.
- Ο αριθμός-f όπως προκύπτει και από τον ορισμό του και για έναν συγκεκριμένο φακό ή για συγκεκριμένη εστιακή απόσταση, είναι αντίστροφος της διαμέτρου της οπής του διαφράγματος. Το αναφέραμε και πιο πάνω. Όταν το ένα μεγαλώνει, ο άλλος μικραίνει. Και αντιστρόφως, όταν ο ένας μικραίνει, το άλλο μεγαλώνει.
- Επειδή ακριβώς υπάρχει αυτή η αντιστροφή, δεν λέμε ποτέ «θα βάλω μεγάλο διάφραγμα». Γιατί αμέσως θα σε ρωτήσω: Εννοείς μεγάλο αριθμό-f ή μεγάλη οπή διαφράγματος; Το σωστό λοιπόν, και για να μιλάμε την ίδια γλώσσα, είναι να λέμε: Βάζω μεγάλο αριθμό-f ή κλείνω το διάφραγμα. Και αντίστροφα, βάζω μικρό αριθμό-f ή ανοίγω το διάφραγμα. Δεν λέμε μικρό ή μεγάλο διάφραγμα. Λέμε κλειστό ή ανοιχτό διάφραγμα. Το “μεγάλο” και το “μικρό” ας το αφήσουμε να το χρησιμοποιούμε για τον αριθμό-f.
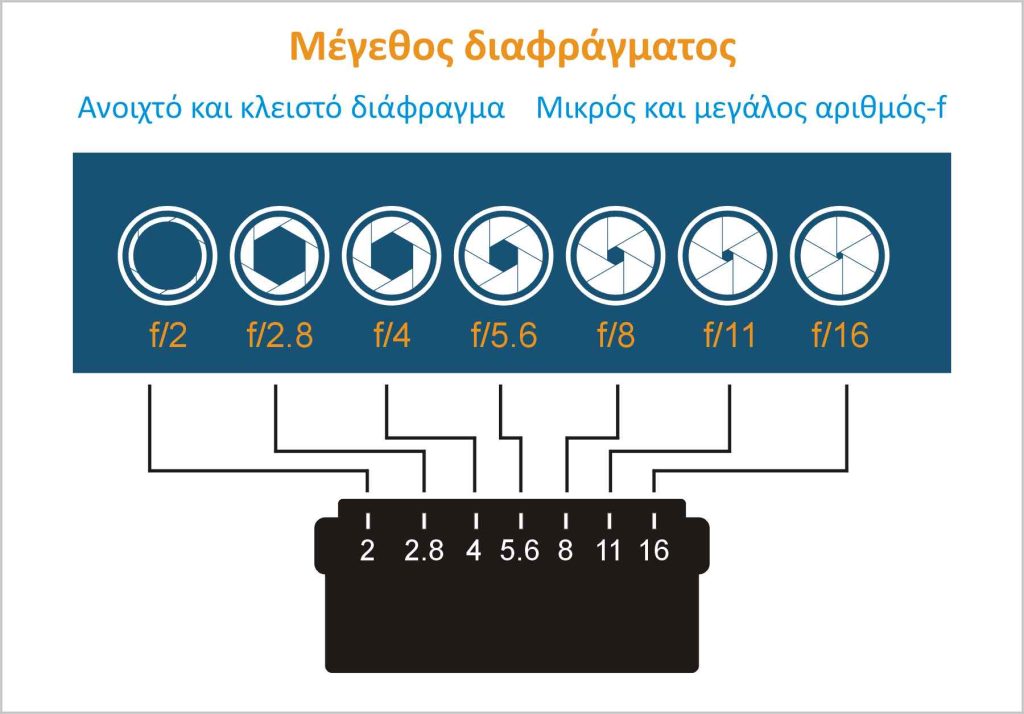
Και πάλι μαθηματικά τώρα. Δεν γίνεται αλλιώς. Αλλά είμαι σίγουρος πως θα το πιάσετε… Θα βοηθήσει και η παραπάνω εικόνα με το “κλειστό” και “ανοιχτό” διάφραγμα.
Θα μου πείτε πως σας “απαγόρευσα” να χρησιμοποιείτε τον όρο “μεγάλο” ή “μικρό” διάφραγμα… Στην πραγματικότητα όμως δεν είναι έτσι… Βεβαίως και μπορούμε να λέμε μεγάλο ή μικρό διάφραγμα αλλά εξαρτάται πώς αναφερόμαστε στον αριθμό-f ! Και για να το πω κι αλλιώς, στην ουσία όταν λέμε μεγάλο και μικρό αναφερόμαστε ορθά, στην μεγάλη και μικρή διάμετρο (της κόρης) του διαφράγματος.
Πάμε πάλι στον ορισμό του αριθμού-f του διαφράγματος και με τη βοήθεια του παρακάτω σχήματος θα δούμε τη σχέση του με τη διάμετρό του: (το κάναμε και πριν αυτό που δείξαμε την αντιστροφή, απλώς εδώ το εξειδικεύουμε και το συνδέουμε με τον τρόπο που δηλώνουμε τον αριθμό-f. Δώστε και πάλι την προσοχή σας.)

Αν “λύσουμε” τον μαθηματικό τύπο ορισμού του αριθμού-f ως προς τη διάμετρο D (D=κόρη εισόδου, μην το ξεχνάμε), τότε βρίσκουμε πως Διάμετρος=f/N
Διάμετρος = D = \frac{f}{αριθμός-f}
Για παράδειγμα λέμε Διάμετρος = f/8. Προσέξτε εδώ τον τρόπο που γράψαμε τη διάμετρο σε σχέση με τον αριθμό-f. Διάμετρος ίσον εφ διά 8, κλάσμα δηλαδή ! Ακριβώς όπως μας έχουν πει να δηλώνουμε τον αριθμό-f !
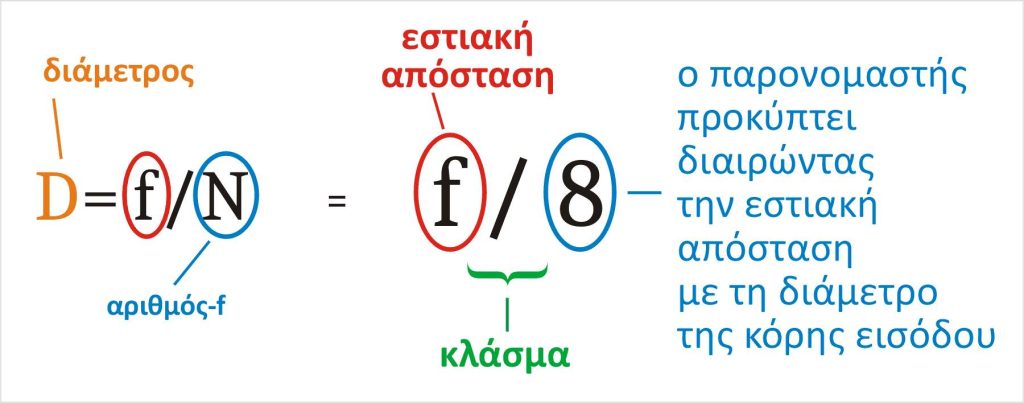
Όταν λοιπόν γράφουμε τον αριθμό-f ως f/N (ως κλάσμα) τότε μπορούμε να πούμε ότι δεν μιλάμε πια για τον αριθμό-f, το Ν δηλαδή, αλλά έχουμε ουσιαστικά εκφράσει το μέγεθος της διαμέτρου του διαφράγματος το D, σε σχέση με την εστιακή απόσταση του φακού f και τον αριθμό-f.
Και επειδή ο αριθμός-f βρίσκεται πάντα στον παρονομαστή του κλάσματος f/N (γράφεται και f:N) είναι φανερό ότι το f/2 (“εφ” δεύτερα) είναι πολύ μεγαλύτερο από το f/16 (“εφ” δέκατα έκτα).
Να λοιπόν τί να προσέξουμε: Ενώ δεν είναι σωστό να λέμε έβαλα μεγάλο διάφραγμα 16 (σκέτο το 16) είναι σωστό να πούμε ότι έβαλα “μικρό διάφραγμα f/16″ (προφορικά δηλαδή, βάζουμε μπροστά από τον αριθμό 16, το f, και το προφέρουμε ως “έφ” μαζί με τον αριθμό ως “εφ δεκαέξι”, υποδηλώνοντας ότι πρόκειται για κλάσμα, για διαίρεση δηλαδή, και άρα, και μικρότερο αριθμό).
Να το πω κι αλλιώς:
Άλλο είναι να πω “έβαλα μεγάλο διάφραγμα δεκαέξι” και άλλο αν πω “έβαλα μικρό διάφραγμα εφ δεκαέξι“. Στην πρώτη περίπτωση είμαι λάθος γιατί αναφέρομαι στον αριθμό-f (και όχι στο διάφραγμα) και στη δεύτερη περίπτωση είμαι σωστός γιατί αναφέρομαι στη διάμετρο του διαφράγματος, σε κλάσμα που είναι όντως “μικρό” ή τελοσπάντων μικρότερο από τον αριθμό-f που πάει στον παρονομαστή του κλάσματος και διαιρεί την εστιακή απόσταση.
Θα μου πείτε τότε γιατί δεν αναγράφονται αυτοί οι αριθμοί-f πάνω στους φακούς με το f μπροστά. Αυτό συμβαίνει αφενός γιατί πάνω στους φακούς γράφουμε τους αριθμούς-f του διαφράγματος και όχι διαμέτρους αλλά και για να μπορούμε πιο εύκολα να χαράξουμε τους αριθμούς στον περιορισμένο χώρο που έχουμε πάνω στο φακό, για εργονομία δηλαδή. Και γιατί τα ευκόλως εννοούμενα παραλείπονται…
Γενικά πάντως, καλό είναι να χρησιμοποιούμε τους όρους “ανοικτό” και “κλειστό” για το διάφραγμα αντί του “μεγάλο” και “μικρό” για να μην μπερδευόμαστε.

Ωραία μέχρι εδώ. Πάμε να δούμε τώρα, πέρα από αυτή τη… “διαστροφική σχέση” αντιστροφής του αριθμού-f με το διάφραγμα, γιατί να είναι και “περίεργος”. Αναφέρομαι στην “περίεργη” σειρά των αριθμών-f που παράλληλα είναι δύσκολο και να τους θυμόμαστε.
Ο αριθμός-f δεν είναι στην πραγματικότητα περίεργος. Μας βολεύει που είναι αυτός που είναι…
Ο περίεργος αριθμός-f, η διάμετρος (σε σχέση) με το εμβαδό (της τρύπας) και η τετραγωνική ρίζα του δύο…
Σας «έκαψα» με τον παραπάνω τίτλο; Να το πάρουμε λίγο χαλαρά; Σας έχω και ένα «δωράκι» μετά.
Ας υποθέσουμε πως θέλετε να τραβήξετε μία σκηνή που φωτίζεται αρκετά. Θέλετε, σύμφωνα με την εκτίμησή σας ή με την εκτίμηση του φωτομέτρου της μηχανής σας να “κόψετε” φως. Να φωτιστεί η σκηνή σας με το μισό φως από αυτό που ήδη έχετε γιατί είναι υπερφωτισμένη.
Κρατήστε εδώ την έκφραση “μισό φως”. Έχει σημασία.

Ωραία θα μου πείτε. Θα κάνω έκθεση στον μισό χρόνο και θα είναι όλα καλά!
Σωστά!
Αν έχετε π.χ. ρυθμίσει ταχύτητα φωτοφράκτη 1/250, θα την βάλετε στο 1/500 και η έκθεση θα είναι η επιθυμητή. Ή, αλλιώς, έχετε αυτή τη δυνατότητα, θα ΚΛΕΙΣΕΤΕ το διάφραγμα έτσι ώστε να αφήσετε να περάσει το μισό φως μέσα από την οπή του!
Ωραία. Τέλεια! Πόσο πρέπει να κλείσετε το διάφραγμα για να πάρετε το μισό φως;
Για να περάσει το μισό φως μέσα από την οπή του διαφράγματος αρκεί το άνοιγμα, το εμβαδό δηλαδή της οπής (προσοχή εδώ, όχι η διάμετρος), να μειωθεί στο μισό.
Σωστά; Και τί σχήμα έχει η οπή του διαφράγματος; Κυκλική δεν είναι; Και πώς όταν έχουμε έναν κύκλο βρίσκουμε τον αμέσως μικρότερο κύκλο που είναι ο μισός του πρώτου;
Μα με τα μαθηματικά!
Και το εμβαδό του κύκλου, έχει κάποια σχέση με τη διάμετρό του. Έτσι μας λένε τα μαθηματικά. Αλλά και η διάμετρος, έχει σχέση με εκείνον που εδώ και ώρα μιλάμε. Με τον αριθμό-f.
Πάμε να δούμε αυτή τη σχέση και γιατί αυτός ο αριθμός είναι “περίεργος”. Χάθηκε να’ ναι ένας αριθμός απλός; 1,2,3,4,5 κάτι τέτοιο βρε αδερφέ. Ε, δεν γινόταν αλλιώς, τί να κάνουμε. Έτσι λένε τα μαθηματικά και τα μαθηματικά δεν είναι εφεύρεση δική μας. Είναι η ίδια η φύση.
Μια μικρή στάση εδώ πριν εξετάσουμε το παραπάνω μαθηματικό πρόβλημα που μας δημιουργήθηκε. Δηλαδή το πώς θα βρούμε έναν κύκλο ο οποίος θα είναι (σε επιφάνεια) ο μισός του πρώτου. Πέρα λοιπόν από τα μαθηματικά, είναι αναγκαίο να έχουμε έναν αριθμό που θα μας βολεύει γενικά στους υπολογισμούς της έκθεσης στη φωτογραφία. Είναι πολλές οι μεταβλητές που ρυθμίζουν την ποσότητα του φωτός. (Να σας τις θυμίσω: Χρόνος έκθεσης, Διάφραγμα, και ευαισθησία ISO). Ταυτόχρονα όμως υπάρχει και η ανάγκη να φτιάχνουμε πρότυπα έτσι ώστε να μην κάνει ο καθένας ότι θέλει και να μπορούμε να μιλάμε την ίδια τεχνική γλώσσα.
Στην αναζήτηση λοιπόν αυτού του αριθμού-f, ας ξεκινήσουμε πρώτον, με τι αριθμό θέλουμε. Και δεύτερον, γιατί τον θέλουμε με αυτά τα χαρακτηριστικά:
- Τί αριθμό θέλουμε:
Θέλουμε έναν (απλό) αριθμό που όταν τον αλλάζουμε να μπορούμε να ελέγχουμε το μέγεθος της οπής του διαφράγματος έτσι ώστε να αφήνουμε να περάσει μέσα από την τρύπα ποσότητα φωτός διπλάσια (ή την μισή). Και δεν αρκεί να μιλάμε μόνο με την διάμετρο της οπής για δύο λόγους:
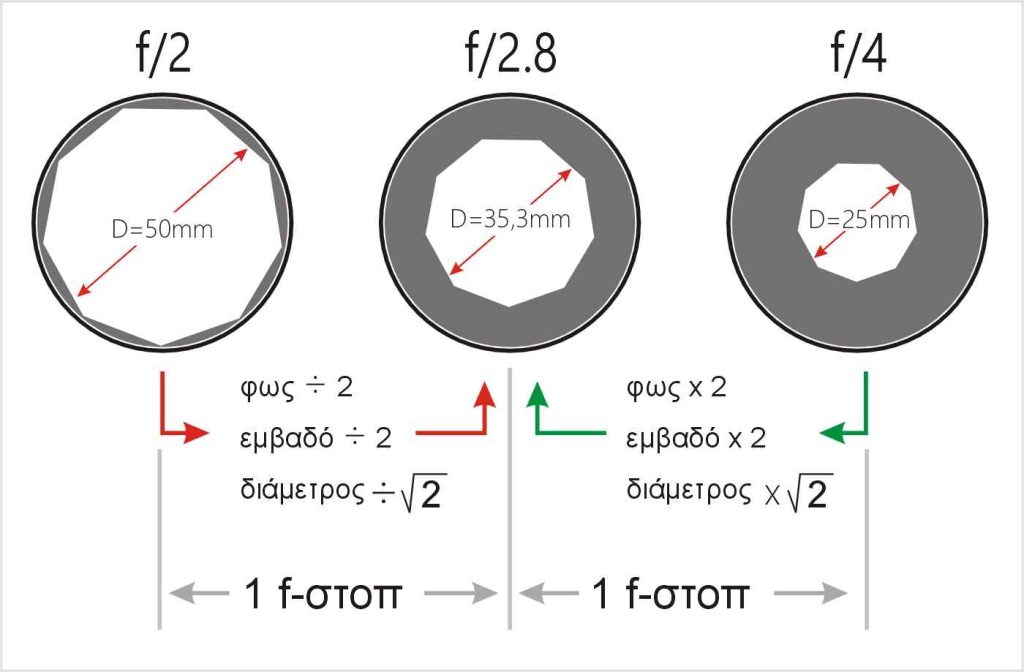
Πρώτον, πρέπει να μιλάμε με εμβαδό, με επιφάνεια δηλαδή. Το μέγεθος της οπής, το εμβαδό της επιφάνειας, είναι το τετράγωνο της διαμέτρου. Ας το δούμε με ένα παράδειγμα: Αν διπλασιάσουμε την διάμετρο της κυκλικής οπής και κάνουμε τους υπολογισμούς σύμφωνα με τον τύπο που μας δίνει το εμβαδό του κύκλου, θα διαπιστώσουμε ότι αυτή η επιφάνεια της οπής, το εμβαδόν του ανοίγματος, τετραπλασιάζεται.
Δεν μας κάνει!
Και δεύτερον, θέλουμε έναν αριθμό τέτοιο, που να σχετίζεται και με την εστιακή απόσταση του φακού.
Και γιατί αυτό;
Αυτό γιατί για διαφορετική εστιακή απόσταση θέλουμε διαφορετική διάμετρο ανοίγματος του διαφράγματος. Αυτό είναι λογικό, γιατί για παράδειγμα, σε έναν τηλεφακό (μεγαλύτερη εστιακή απόσταση), έχουμε μεγαλύτερη μεγέθυνση. Που σημαίνει ότι για να πάρουμε το ίδιο φως που παίρνουμε με έναν ευρυγώνιο φακό (μικρή εστιακή απόσταση) θα πρέπει στον τηλεφακό, να έχουμε πιο μεγάλο άνοιγμα σε σχέση με τον ευρυγώνιο. Αν αυτό δεν έγινε άμεσα αντιληπτό, με τον τηλεφακό και τον ρόλο της μεγέθυνσης στην ποσότητα του φωτός αφήστε το για αργότερα. Θα το δούμε με ένα παράδειγμα στο επόμενο μέρος του άρθρου. - Γιατί θέλουμε έναν τέτοιο αριθμό:
Θέλουμε έναν αριθμό με αυτά τα χαρακτηριστικά (διπλασιασμού ή υποδιπλασιασμού του φωτός) έτσι ώστε να μπορούμε να τον συσχετίσουμε με ευκολία με τον χρόνο έκθεσης που και αυτόν τον επιλέγουμε με τα ίδια κριτήρια (διπλασιασμού ή υποδιπλασιασμού του φωτός).
Άρα, θέλουμε να βρούμε εκείνον τον αριθμό που διπλασιάζει ή υποδιπλασιάζει το εμβαδό αλλά σχετίζεται με τη διάμετρο του ανοίγματος του διαφράγματος ανεξάρτητα από την εστιακή απόσταση του φακού.
Ε λοιπόν αυτός ο αριθμός είναι ο \sqrt{2}=1,4142135.
Πάρτε τον έτσι, “δωράκι” από εμένα. Χωρίς μαθηματικά… (Όχι, δεν θα τη γλιτώσετε. Θα κάνουμε μετά την απόδειξη).
Ας δούμε πρώτα πώς θα χρησιμοποιήσουμε αυτό το \sqrt{2}. Ας προσέξουμε καλά την επόμενη παράγραφο:
Κάθε φορά που θέλουμε να αλλάξουμε την έκθεση ελεγχόμενα και ακριβώς επί δύο ή διά δύο, (ανοίγοντας ή κλείνοντας το διάφραγμα αντίστοιχα) αρκεί να μεγαλώσουμε ή να μικρύνουμε τη διάμετρο της οπής του κατά 1,4142135 φορές !
Απαντάμε έτσι και στο πρόβλημα που θέσαμε πριν, για το πώς θα βρούμε ένα κύκλο που θα είναι π.χ. ο μισός του πρώτου κύκλου. Αρκεί να διαιρέσουμε τη διάμετρό του με την τετραγωνική ρίζα του δύο ( \sqrt{2}) που είναι ίση με 1,4142135.
Παρένθεση: Κάπως έτσι “γεννήθηκε” το f-στοπ… Εντάξει… δεν γεννήθηκε με αυτόν τον τρόπο, και όσο και αν το έψαξα δεν υπάρχει σαφής αναφορά για το πότε ξεκίνησε να χρησιμοποιείται ο όρος «f-stop». Αλλά με την ευκαιρία να πούμε και το εξής σημαντικό: Όταν λέμε f-στοπ, είναι διαφορετικό από το στοπ σκέτο. Όταν λέμε ένα f-στοπ, αναφερόμαστε στην έκθεση μεν, αλλά αυτό, αφορά πάντα, το διάφραγμα. Όταν λέμε στοπ (σκέτο, χωρίς το εφ μπροστά) πάλι αναφερόμαστε στην έκθεση αλλά σε αυτή την περίπτωση δηλώνουμε γενικά τη διαφορά στην έκθεση (διπλάσιο ή το μισό φως). Και να πούμε επίσης πως η χρήση του αριθμού-f δεν ήταν στο παρελθόν η μοναδική μέθοδος για τον καθορισμό των ρυθμίσεων του διαφράγματος. Κάθε κατασκευαστής προσπαθούσε να κάνει το δικό του πρότυπο. Αλλά είπαμε, αυτό είναι παρελθόν.

Πάμε τώρα να το δούμε με ένα παράδειγμα αυτό που είπαμε πριν, τον πολλαπλασιασμό (και τη διαίρεση) της διαμέτρου με τον αριθμό \sqrt{2} :
Έχουμε έναν φακό, ας πούμε 50 χιλιοστά και έχουμε “βάλει διάφραγμα” f/4. Δεν θέλουμε να αλλάξουμε τον χρόνο λήψης γιατί ήδη είναι πολύ μεγάλος, ας υποθέσουμε 1/60 και φοβόμαστε πως η φωτογραφία θα μας βγει “κουνημένη”. Έχουμε λοιπόν περιθώρια να ανοίξουμε το διάφραγμα ρυθμίζοντάς το με αριθμό-f=2.8 η αλλιώς ένα f-στοπ πάνω. Πώς προέκυψε αυτό; Μα με διαίρεση του αριθμού-f = 4 με τον “μαγικό αριθμό” δωράκι που σας έκανα: 4 διά \sqrt{2} = 4 διά 1,4142135 ίσον με 2.8 !
Και πάλι όμως εδώ ΠΡΟΣΟΧΗ. Θυμηθείτε την αντίστροφη σχέση του αριθμού-f με τη διάμετρο:
Είπαμε όταν πάμε ένα f-stop πάνω, δηλαδή διπλάσιο φως, επειδή διπλασιάσαμε το εμβαδό της οπής του διαφράγματος, πολλαπλασιάσαμε τη διάμετρο με ρίζα δύο. Αντίστοιχα όμως και επειδή ο αριθμός-f είναι αντίστροφος της διαμέτρου, διαιρέσαμε τον αριθμό-f με τη ρίζα του δύο. Γι’ αυτό και μικρότερος αριθμός-f. Σε αυτό το σημείο είναι όλη η ιστορία και εδώ γεννιέται όλη η σύγχυση.
Έχουμε λοιπόν:
α) όταν πάμε ένα f-stop πάνω:
Όταν αναφερόμαστε στη διάμετρο, την πολλαπλασιάζουμε με \sqrt{2} και όταν αναφερόμαστε στον αριθμό-f, τον διαιρούμε με \sqrt{2}.
Και αντίστοιχα, (αλλά και αντίστροφα):
b) όταν πάμε ένα f-στοπ κάτω:
Όταν αναφερόμαστε στη διάμετρο, την διαιρούμε με \sqrt{2} και όταν αναφερόμαστε στον αριθμό-f, τον πολλαπλασιάζουμε με \sqrt{2}.
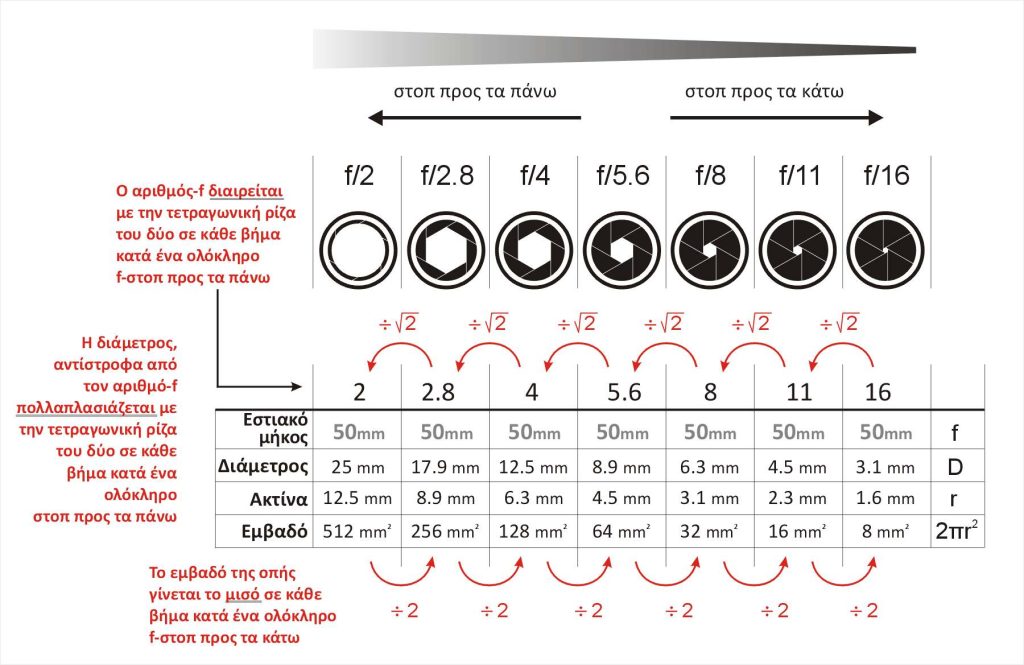
Πριν προχωρήσουμε ακόμα περισσότερο με αυτόν τον μαγικό αριθμό-f, πρέπει να προσέξουμε κάτι και να το κάνουμε απόλυτα κατανοητό. Και μέσα από αυτό να κατανοήσουμε και το ΓΙΑΤΙ έχουμε επιλέξει τον συγκεκριμένο αριθμό-f:
Κάθε φορά που “παίζουμε” με το διάφραγμα, κοιτάζουμε να αυξάνουμε (ή να μειώνουμε) την έκθεση σε “βήματα” που (κατά κανόνα) είναι βήματα που το ένα από το άλλο “απέχει” ένα ολόκληρο f-στοπ. (Εντάξει, υπάρχουν και οι «υποδιαιρέσεις του f-στοπ, αλλά ας το αφήσουμε προς το παρόν).

Να το πούμε και ανάποδα, γιατί πρέπει να καταλάβουμε ότι αν και ο αριθμός-f σχετίζεται με τον συντελεστή \sqrt{2} ή 1,4142135 εκείνο που συμβαίνει είναι πάντα, είτε ένας πολλαπλασιασμός (του φωτός που επιτρέπουμε να περάσει από την οπή του διαφράγματος) επί δύο ή μία διαίρεση του φωτός διά δύο. Και κάθε ένα τέτοιο βήμα, όπως είδαμε, είναι ένα “ολόκληρο f-στοπ”. Μπορεί η σχέση της ποσότητας του φωτός να είναι επί 2, επί 4, επί 8, επί 16 κ.ο.κ. όμως η σχέση της ΔΙΑΜΕΤΡΟΥ του διαφράγματος είναι επί {\sqrt{2}}, επί 2 φορές {\sqrt{2}}, επί 3 φορές {\sqrt{2}}, επί 4 φορές {\sqrt{2}} κ.ο.κ.
Επιμένω και θα το πω και αλλιώς με δύο παραδείγματα έκθεσης κατά ένα και δύο f-stop προς τα πάνω και προς τα κάτω:
Πρώτο παράδειγμα με ένα και δύο f-stop προς τα πάνω:
Πάμε ένα (1) f-στοπ πάνω, σημαίνει (και συμβαίνουν) τα εξής:
- Διπλασιάζουμε το εμβαδό της οπής του διαφράγματος (επί 2)
- Διπλασιάζουμε το φως (επί 2)
- Πολλαπλασιάζουμε τη διάμετρο του διαφράγματος με το \sqrt{2} (επί 1.41421)
- Διαιρούμε τον αριθμό-f με το \sqrt{2} (διά 1.41421)
Πάμε δύο (2) f-στοπ πάνω, σημαίνει (και συμβαίνουν) τα εξής:
- Τετραπλασιάζουμε το εμβαδό της οπής του διαφράγματος (2 επί 2 = επί 4)
- Τετραπλασιάζουμε το φως (2 επί 2 = επί 4)
- Πολλαπλασιάζουμε τη διάμετρο του διαφράγματος δύο φορές με το \sqrt{2} οπότε: 2 x \sqrt{2} = \sqrt{2}^2 = 2 (άρα διάμετρος επί 2)
- Διαιρούμε τον αριθμό-f δύο φορές με το \sqrt{2} οπότε \frac{αριθμός-f}{\sqrt{2}^2} = \frac{αριθμός-f}{2} (άρα αριθμός-f διά δύο)
Και αλλιώς: κάθε φορά που κάνουμε ένα κλικ στο διάφραγμα κατά ένα f-στοπ προς τα πάνω έχουμε φως επί 2, επί 4, επί 8, επί 16, επί 32 κ.ο.κ. και όχι επί 1, επί 2, επί 3, επί 4, επί 5 κ.ο.κ.
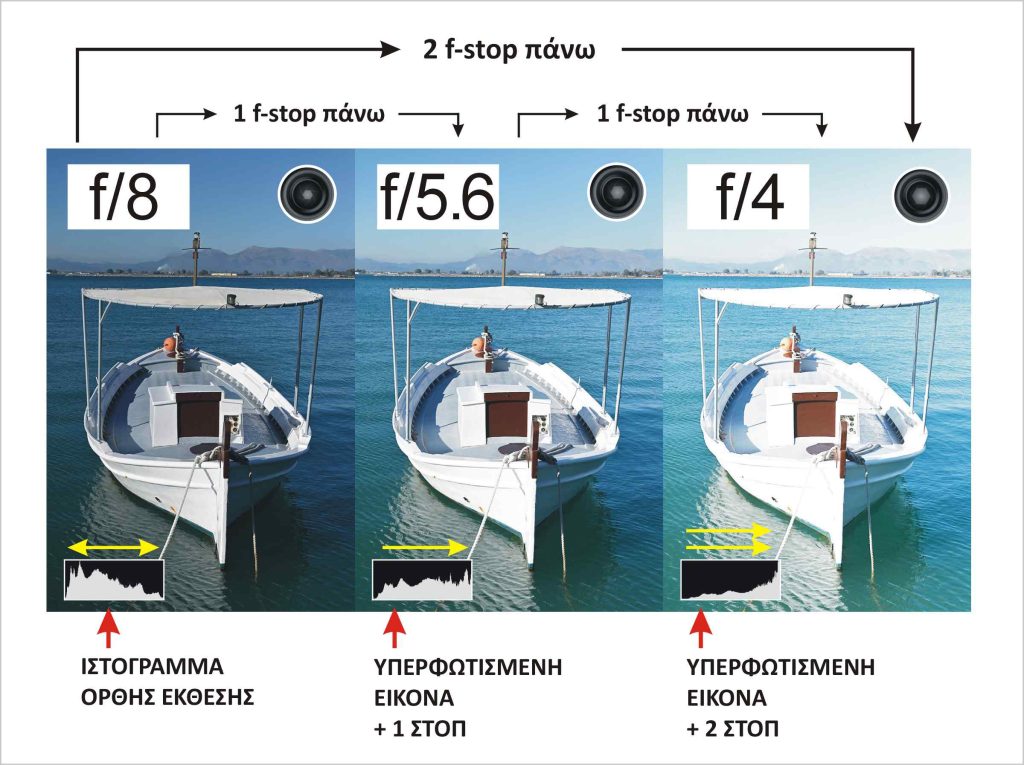
Δεύτερο παράδειγμα με ένα και δύο f-stop προς τα κάτω:
Πάμε ένα (1) f-στοπ κάτω, σημαίνει (και συμβαίνουν) τα εξής:
- Κάνουμε μισό το εμβαδό της οπής του διαφράγματος (διά 2)
- Παίρνουμε το μισό φως στον αισθητήρα (διά 2)
- Διαιρούμε τη διάμετρο του διαφράγματος με \sqrt{2} (διά 1.41421)
- Πολλαπλασιάζουμε τον αριθμό-f με \sqrt{2} (επί 1.41421)
Πάμε δύο (2) f-στοπ κάτω, σημαίνει (και συμβαίνουν) τα εξής:
- Το εμβαδό του διαφράγματος είναι το ένα τέταρτο (2 φορές διά δύο = διά 4)
- Παίρνουμε το ένα τέταρτο του φωτός στον αισθητήρα (2 φορές διά δύο = διά 4)
- Διαιρούμε τη διάμετρο του διαφράγματος δύο φορές με \sqrt{2} που είναι 2\frac{D}{\sqrt{2}} = \frac{D}{\sqrt{2}} \frac{D}{\sqrt{2}} = \frac{D}{(\sqrt{2})^2} = με \frac{D}{2} δηλαδή έχουμε τη μισή διάμετρο.
- Πολλαπλασιάζουμε δύο φορές τον αριθμό-f με \sqrt{2} που είναι αριθμός-f επί 2\sqrt{2} = αριθμός-f επί {(\sqrt{2})^2} = αριθμός-f επί δύο. Ή αλλιώς όταν πάμε δύο f-στοπ κάτω, ο αριθμός-f διπλασιάζεται.
Και αλλιώς: κάθε φορά που κάνουμε ένα κλικ στο διάφραγμα κατά ένα f-στοπ προς τα κάτω έχουμε φως διά 2, διά 4, διά 8, διά 16, διά 32 κ.ο.κ. και όχι διά 1, διά 2, διά 3, διά 4, διά 5 κ.ο.κ.

Τώρα:
Προσέξτε αυτή τη σχέση μεγεθών μεταξύ των f-στοπ που είναι επί 2, επί 4, επί 8, επί 16, επί 32 κ.ο.κ. Γιατί θέλουμε αυτή τη σχέση;
Την θέλουμε για να μπορούμε να συσχετίζουμε το διάφραγμα με τον χρόνο έκθεσης. Και αυτό, γιατί στην έκθεση υπάρχει η αρχή της αμοιβαιότητας.
Άντε πάλι… “Έσκασε” ένας καινούργιος όρος. Αλλά είμαι σίγουρος πως αυτή την “αρχή αμοιβαιότητας” την γνωρίζετε ήδη, τουλάχιστον πρακτικά.
Η αρχή της αμοιβαιότητας στην έκθεση του μέσου
Ας πάμε τώρα σε αυτή την “αρχή αμοιβαιότητας”. Απλό είναι, και η αρχή αυτή, “κατάγεται” από τότε που τραβάγαμε φωτογραφίες με φιλμ, αλλά, ισχύει και σήμερα με τους αισθητήρες. Αφορά την συνεισφορά των μεγεθών α) χρόνος έκθεσης, β) φως στη μονάδα του χρόνου και γ) ευαισθησία του φιλμ (ή του αισθητήρα) στην έκθεση.
Πρακτικά αν μιλήσουμε για την αρχή αμοιβαιότητας μπορούμε να πούμε πως για δεδομένη ευαισθησία του φιλμ ή για δεδομένο ISO στην ψηφιακή μας φωτογραφική μηχανή, ή έκθεση που θα κάνουμε, με ένα ζευγάρι ρυθμίσεων χρόνου έκθεσης και διαφράγματος, θα είναι ισοδύναμη με ένα άλλο ζευγάρι ρυθμίσεων χρόνου έκθεσης και διαφράγματος αρκεί να αλλάξουμε κάποια παράμετρο της έκθεσης αμοιβαία. Αν για παράδειγμα διπλασιάσουμε τον χρόνο έκθεσης θα πρέπει αμοιβαία να υποδιπλασιάσουμε το άνοιγμα του διαφράγματος (με άλλα λόγια αν πάμε ένα στοπ πάνω τον χρόνο έκθεσης θα πρέπει αμοιβαία να πάμε ένα f-στοπ κάτω το διάφραγμα).
Τα παρακάτω ζεύγη ρυθμίσεων στη μηχανή μας θα έχουν ακριβώς* τα ίδια αποτελέσματα στην έκθεση (*το ακριβώς δεν ισχύει αλλά μην μιλήσουμε τώρα και για το reciprocity failure)
Χρόνος t=\frac{1}{250}δευτ. & διάφραγμα f/2.8 ισοδύναμο ⇒
Χρόνος t=\frac{1}{125}δευτ. & διάφραγμα f/4 ισοδύναμο ⇒
Χρόνος t=\frac{1}{60}δευτ. & διάφραγμα f/5.6
Εάν κάποιος εκθέσει το φιλμ ή τον αισθητήρα για μεγαλύτερο χρονικό διάστημα, απαιτείται αμοιβαία μικρότερο άνοιγμα διαφράγματος για να μειωθεί η ποσότητα φωτός που φτάνει στο φιλμ και να λάβει την ίδια έκθεση.
Και επειδή μας αρέσει η τάξη, ας βάλουμε τώρα όλους του πιθανούς αριθμούς-f στη σειρά έτσι για να τους ευχαριστηθούμε:
f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f/22, f/32, f/45, f/64, f/90, f/128 κ.λ.π.
Αριθμοί-f που προκύπτουν από:
f/1=\large \frac{f}{(\sqrt{2})^0}\normalsize \quad f/1.4=\large \frac{f}{(\sqrt{2})^1}\normalsize \quad f/2=\large \frac{f}{(\sqrt{2})^2}\normalsize \quad f/2.8=\large \frac{f}{(\sqrt{2})^3}\normalsize \quad f/4=\large \frac{f}{(\sqrt{2})^4}\normalsize \quad f/5.6=\large \frac{f}{(\sqrt{2})^5} \normalsize \dots κ.λ.π.
Και πώς θα τους θυμόμαστε;
Η απομνημόνευση της σειράς των αριθμών-f
Επειδή δεν είναι και τόσο εύκολο να θυμόμαστε όλη τη σειρά των αριθμών-f, θα κάνουμε ένα «κόλπο». Θα την «σπάσουμε» τη σειρά των αριθμών-f και θα τους τοποθετήσουμε σε δύο σειρές, όχι σε μία.
Δείτε το επόμενο σχήμα. Με αυτή τη διάταξη ο κάθε ένας αριθμός-f θα “απέχει” από τον γειτονικό του όχι ένα f-στοπ αλλά δύο f-στοπ. Αρκεί τότε, να θυμόμαστε μόνο δύο από τους αριθμούς αυτούς. Τον f/1 και τον f/1.4. Διπλασιάζοντας εναλλάξ κάθε φορά τους δύο παραπάνω αριθμούς-f βρίσκουμε όλη τη σειρά.
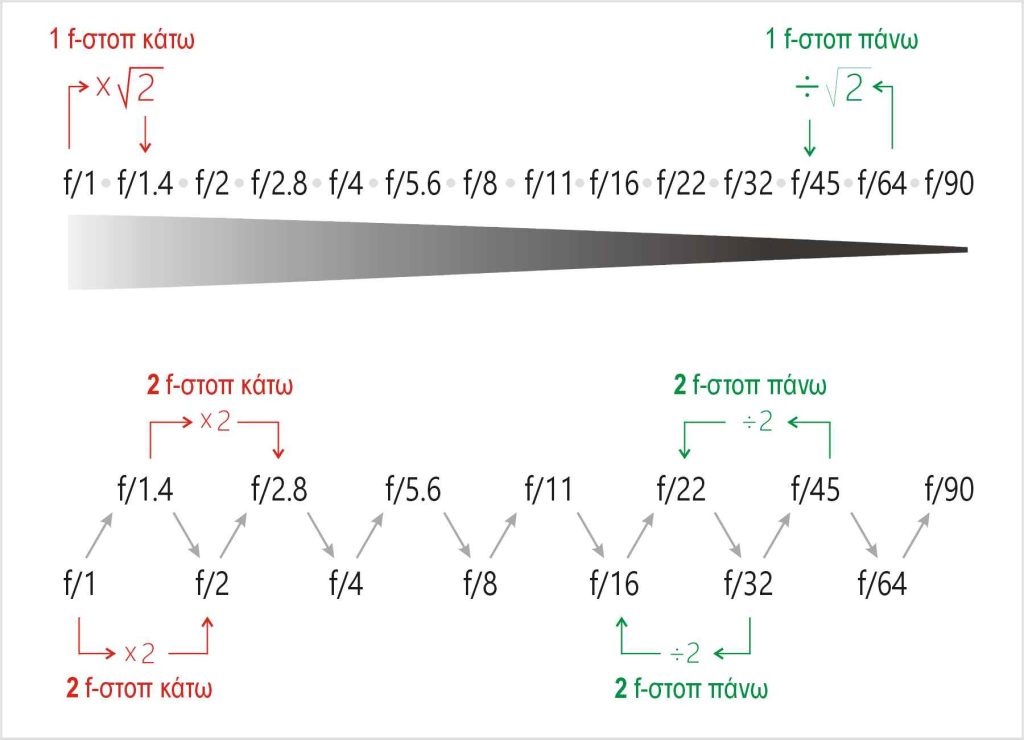
Νομίζω γίνεται εύκολα κατανοητό ότι όταν πάμε σε τέτοια ζεύγη και επειδή πολλαπλασιάζουμε δύο φορές την τετραγωνική ρίζα του δύο, γίνεται τετραγωνική ρίζα του δύο στο τετράγωνο, και άρα, μας μένει σκέτο το δύο! Και έτσι είναι πιο εύκολη η απομνημόνευση όλης της σειράς των αριθμών-f.
Και μιας και μας αρέσει να τα έχουμε όλα τακτοποιημένα, ας βάλουμε σε μία σειρά και τους πιθανούς χρόνους έκθεσης σε δευτερόλεπτα, για να διαπιστώσουμε πως και εδώ, έχουμε μία σχέση μεταξύ τους επί 2, επί 4, επί 8, επί 16, επί 32 κ.ο.κ. με αποτέλεσμα να έχει ο κάθε αριθμός ένα στοπ διαφορά, με τους γειτονικούς του:
\large\frac{1}{1000}s\enspace\frac{1}{500}s\enspace\frac{1}{250}s\enspace\frac{1}{125}s\enspace\frac{1}{60}s\enspace\frac{1}{30}s\enspace\frac{1}{15}s\enspace\frac{1}{8}s\enspace\frac{1}{4}s\enspace\frac{1}{2}s\enspace1s
Και αν παραθέσουμε και τους αριθμούς ISO θα έχουμε κάνει μία ομορφιά:
100, 200, 400, 800, 1600, 3200, 6400, 12800, 25600, 51200, 102400 κ.ο.κ.
όπου και εδώ έχουμε μία σχέση μεταξύ τους κατά ένα στοπ (επί 2, επί 4, επί 8, επί 16, επί 32 κ.ο.κ.).
Δεν είναι απαραίτητο πιστεύω να αναλύσουμε περισσότερο πώς προέκυψαν οι αριθμοί ISO που μετράνε την ευαισθησία του μέσου καταγραφής της εικόνας (φιλμ ή αισθητήρας) και ουσιαστικά μας δείχνουν την “ταχύτητά” τους, δηλαδή πόσο γρήγορα καταγράφουν την εικόνα στη μονάδα του χρόνου. Οι αριθμοί ISO είναι κληρονομιά από την εποχή του φιλμ και δεν είναι το μοναδικό στάνταρ για την προτυποποίηση της ταχύτητάς τους. Οι παλιότεροι θα θυμούνται τα ASA…
Αν θυμηθούμε τώρα την αρχή αμοιβαιότητας που είπαμε πριν, και έχοντας μέσα στο “παιχνίδι” της έκθεσης και τους αριθμούς ISO, μπορούμε να έχουμε μία τριάδα πλέον τιμών (διαφράγματος, χρόνου, και ISO) για τις οποίες η έκθεση θα είναι ισοδύναμη. Κάποιοι θα θυμηθούν εδώ το “τρίγωνο της έκθεσης”.
Όπως και να το κάνουμε, τα τρίγωνα είναι “ωραία”… Και στη φωτογραφία !
Νιώθω όμως ότι σας έχω κουράσει και πως οι πληροφορίες είναι πολλές. Θα “σπάσω” αυτό το άρθρο σε δύο μέρη. Πιστεύω πως το θέμα με το διάφραγμα δεν μπορεί να καλυφθεί σε ένα μόνο άρθρο.
Έτσι λοιπόν στο επόμενο θα μιλήσουμε με περισσότερα παραδείγματα για την αρχή αμοιβαιότητας στην έκθεση του μέσου, και από εκεί θα πάμε στη μονάδα EV (exposure value) που είναι κι αυτός ένας αριθμός πιο “ανθρώπινος”.
Επίσης θα αναφερθούμε στις υποδιαιρέσεις του αριθμού-f, ή αλλιώς στα “βήματα” που δεν είναι ολόκληρα f-στοπ και τα οποία βήματα θα βρείτε στις ρυθμίσεις διαφράγματος στις σύγχρονες ψηφιακές φωτογραφικές μηχανές αλλά και στους περισσότερους φακούς.
Δεν θα ξεχάσουμε τον αριθμό-Τ, που είναι σημαντικός στον κινηματογράφο και θα δούμε γιατί δύο ίδιοι φακοί μπορεί να μην έχουν την ίδια “φωτεινότητα” αν και έχουν τον ίδιο αριθμό-f όπως και γιατί κάποιοι φακοί zoom (όχι όλοι) δεν έχουν σταθερό διάφραγμα, δηλαδή το διάφραγμά τους ή αλλιώς ο αριθμός-f δεν παραμένει σταθερός σε όλο το εύρος της εστιακής τους απόστασης.
Θα αναφερθούμε επίσης και σε κάποια άλλα ακόμα θέματα που δεν καλύφθηκαν, όπως τα οπτικά σφάλματα ή “εκτροπές” του φακού, πώς σχετίζονται με τις ρυθμίσεις μας στο διάφραγμα και πώς τις αποφεύγουμε. Όπως και το γιατί σε macro φακούς (που εστιάζουν πολύ κοντά στο θέμα) ό,τι έχουμε πει μέχρι τώρα για το διάφραγμα και και τη φωτεινότητα που φακού “πάει περίπατο”, δεν ισχύει!. Ό,τι αναφέραμε για τον αριθμό-f, ισχύει μόνο για τις περιπτώσεις που ο φακός μας εστιάζει στο άπειρο. Αν και στην πράξη, αυτό παραβλέπεται στη φωτογραφία, δεν μπορούμε να το παραβλέψουμε όταν εστιάζουμε πολύ κοντά ή όταν τοποθετούμε extension tubes ή bellows (φυσούνα) ανάμεσα στον αισθητήρα και τον φακό.

Δεν θα παραλείψουμε να δούμε κάποια παραδείγματα που αφορούν το μέγεθος τον φακών και γιατί (ειδικά οι τηλεφακοί) γίνονται “θηρία” όταν μαζί με την μεγέθυνση έχουν και μεγάλη φωτεινότητα. Όπως και γιατί με τους teleconverters “χάνουμε” κάποια f-στοπ. Και ίσως και πολλά άλλα θέματα που αφορούν το διάφραγμα και μου διαφεύγουν τώρα… Το βλέπω να σπάσει σε τρία μέρη το άρθρο… Ας πρόσεχα !
Θα κλείσω με την μαθηματική απόδειξη με τον διπλασιασμό της επιφάνειας του κύκλου και τον συντελεστή \sqrt{2} όπως σας είχα υποσχεθεί. Ρίξτε μια ματιά. Το ξαναλέω, τα μαθηματικά είναι η ίδια η φύση!
21 Απριλίου 2021, Φάνης Τσίρος



Αφήστε μια απάντηση